What are Convolutional Neural Networks and why are they important?
Convolutional Neural Networks (ConvNets or CNNs) are a category of Neural Networks that have proven very effective in areas such as image recognition and classification. ConvNets have been successful in identifying faces, objects and traffic signs apart from powering vision in robots and self driving cars.
Figure 1: Source [1]
In Figure 1 above, a ConvNet is able to recognize scenes and the system is able to suggest relevant captions (“a soccer player is kicking a soccer ball”) while Figure 2 shows an example of ConvNets being used for recognizing everyday objects, humans and animals. Lately, ConvNets have been effective in several Natural Language Processing tasks (such as sentence classification) as well.
Figure 2: Source [2]
ConvNets, therefore, are an important tool for most machine learning practitioners today. However, understanding ConvNets and learning to use them for the first time can sometimes be an intimidating experience. The primary purpose of this blog post is to develop an understanding of how Convolutional Neural Networks work on images.
If you are new to neural networks in general, I would recommend reading this short tutorial on Multi Layer Perceptrons to get an idea about how they work, before proceeding. Multi Layer Perceptrons are referred to as “Fully Connected Layers” in this post.
The LeNet Architecture (1990s)
LeNet was one of the very first convolutional neural networks which helped propel the field of Deep Learning. This pioneering work by Yann LeCun was named LeNet5 after many previous successful iterations since the year 1988 [3]. At that time the LeNet architecture was used mainly for character recognition tasks such as reading zip codes, digits, etc.
Below, we will develop an intuition of how the LeNet architecture learns to recognize images. There have been several new architectures proposed in the recent years which are improvements over the LeNet, but they all use the main concepts from the LeNet and are relatively easier to understand if you have a clear understanding of the former.
Figure 3: A simple ConvNet. Source [5]
The Convolutional Neural Network in Figure 3 is similar in architecture to the original LeNet and classifies an input image into four categories: dog, cat, boat or bird (the original LeNet was used mainly for character recognition tasks). As evident from the figure above, on receiving a boat image as input, the network correctly assigns the highest probability for boat (0.94) among all four categories. The sum of all probabilities in the output layer should be one (explained later in this post).
There are four main operations in the ConvNet shown in Figure 3 above:
These operations are the basic building blocks of every Convolutional Neural Network, so understanding how these work is an important step to developing a sound understanding of ConvNets. We will try to understand the intuition behind each of these operations below.
An Image is a matrix of pixel values
Essentially, every image can be represented as a matrix of pixel values.
Figure 4: Every image is a matrix of pixel values. Source [6]
Channel is a conventional term used to refer to a certain component of an image. An image from a standard digital camera will have three channels – red, green and blue – you can imagine those as three 2d-matrices stacked over each other (one for each color), each having pixel values in the range 0 to 255.
A grayscale image, on the other hand, has just one channel. For the purpose of this post, we will only consider grayscale images, so we will have a single 2d matrix representing an image. The value of each pixel in the matrix will range from 0 to 255 – zero indicating black and 255 indicating white.
The Convolution Step
ConvNets derive their name from the “convolution” operator. The primary purpose of Convolution in case of a ConvNet is to extract features from the input image. Convolution preserves the spatial relationship between pixels by learning image features using small squares of input data. We will not go into the mathematical details of Convolution here, but will try to understand how it works over images.
As we discussed above, every image can be considered as a matrix of pixel values. Consider a 5 x 5 image whose pixel values are only 0 and 1 (note that for a grayscale image, pixel values range from 0 to 255, the green matrix below is a special case where pixel values are only 0 and 1):
Also, consider another 3 x 3 matrix as shown below:
Then, the Convolution of the 5 x 5 image and the 3 x 3 matrix can be computed as shown in the animation in Figure 5 below: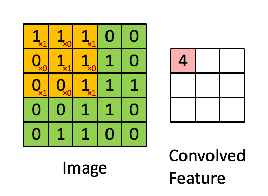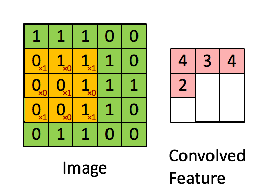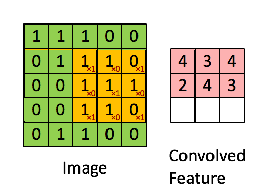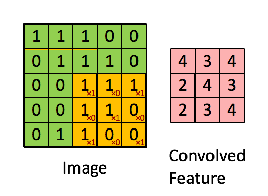
Figure 5: The Convolution operation. The output matrix is called Convolved Feature or Feature Map. Source [7]
Take a moment to understand how the computation above is being done. We slide the orange matrix over our original image (green) by 1 pixel (also called ‘stride’) and for every position, we compute element wise multiplication (between the two matrices) and add the multiplication outputs to get the final integer which forms a single element of the output matrix (pink). Note that the 3×3 matrix “sees” only a part of the input image in each stride.
In CNN terminology, the 3×3 matrix is called a ‘filter‘ or ‘kernel’ or ‘feature detector’ and the matrix formed by sliding the filter over the image and computing the dot product is called the ‘Convolved Feature’ or ‘Activation Map’ or the ‘Feature Map‘. It is important to note that filters acts as feature detectors from the original input image.
It is evident from the animation above that different values of the filter matrix will produce different Feature Maps for the same input image. As an example, consider the following input image:
In the table below, we can see the effects of convolution of the above image with different filters. As shown, we can perform operations such as Edge Detection, Sharpen and Blur just by changing the numeric values of our filter matrix before the convolution operation [8] – this means that different filters can detect different features from an image, for example edges, curves etc. More such examples are available in Section 8.2.4 here.
Another good way to understand the Convolution operation is by looking at the animation in Figure 6 below:
Figure 6: The Convolution Operation. Source [9]
A filter (with red outline) slides over the input image (convolution operation) to produce a feature map. The convolution of another filter (with the green outline), over the same image gives a different feature map as shown. It is important to note that the Convolution operation captures the local dependencies in the original image. Also notice how these two different filters generate different feature maps from the same original image. Remember that the image and the two filters above are just numeric matrices as we have discussed above.
In practice, a CNN learns the values of these filters on its own during the training process (although we still need to specify parameters such as number of filters, filter size, architecture of the network etc. before the training process). The more number of filters we have, the more image features get extracted and the better our network becomes at recognizing patterns in unseen images.
The size of the Feature Map (Convolved Feature) is controlled by three parameters [4] that we need to decide before the convolution step is performed:
Figure 7
Introducing Non Linearity (ReLU)
An additional operation called ReLU has been used after every Convolution operation in Figure 3 above. ReLU stands for Rectified Linear Unit and is a non-linear operation. Its output is given by:
Figure 8: the ReLU operation
ReLU is an element wise operation (applied per pixel) and replaces all negative pixel values in the feature map by zero. The purpose of ReLU is to introduce non-linearity in our ConvNet, since most of the real-world data we would want our ConvNet to learn would be non-linear (Convolution is a linear operation – element wise matrix multiplication and addition, so we account for non-linearity by introducing a non-linear function like ReLU).
The ReLU operation can be understood clearly from Figure 9 below. It shows the ReLU operation applied to one of the feature maps obtained in Figure 6 above. The output feature map here is also referred to as the ‘Rectified’ feature map.
Figure 9: ReLU operation. Source [10]
Other non linear functions such as tanh or sigmoid can also be used instead of ReLU, but ReLU has been found to perform better in most situations.
The Pooling Step
Spatial Pooling (also called subsampling or downsampling) reduces the dimensionality of each feature map but retains the most important information. Spatial Pooling can be of different types: Max, Average, Sum etc.
In case of Max Pooling, we define a spatial neighborhood (for example, a 2×2 window) and take the largest element from the rectified feature map within that window. Instead of taking the largest element we could also take the average (Average Pooling) or sum of all elements in that window. In practice, Max Pooling has been shown to work better.
Figure 10 shows an example of Max Pooling operation on a Rectified Feature map (obtained after convolution + ReLU operation) by using a 2×2 window.
Figure 10: Max Pooling. Source [4]
We slide our 2 x 2 window by 2 cells (also called ‘stride’) and take the maximum value in each region. As shown in Figure 10, this reduces the dimensionality of our feature map.
In the network shown in Figure 11, pooling operation is applied separately to each feature map (notice that, due to this, we get three output maps from three input maps).
Figure 11: Pooling applied to Rectified Feature Maps
Figure 12 shows the effect of Pooling on the Rectified Feature Map we received after the ReLU operation in Figure 9 above.
Figure 12: Pooling. Source [10]
The function of Pooling is to progressively reduce the spatial size of the input representation [4]. In particular, pooling
Figure 13
So far we have seen how Convolution, ReLU and Pooling work. It is important to understand that these layers are the basic building blocks of any CNN. As shown in Figure 13, we have two sets of Convolution, ReLU & Pooling layers – the 2nd Convolution layer performs convolution on the output of the first Pooling Layer using six filters to produce a total of six feature maps. ReLU is then applied individually on all of these six feature maps. We then perform Max Pooling operation separately on each of the six rectified feature maps.
Together these layers extract the useful features from the images, introduce non-linearity in our network and reduce feature dimension while aiming to make the features somewhat equivariant to scale and translation [18].
The output of the 2nd Pooling Layer acts as an input to the Fully Connected Layer, which we will discuss in the next section.
Fully Connected Layer
The Fully Connected layer is a traditional Multi Layer Perceptron that uses a softmax activation function in the output layer (other classifiers like SVM can also be used, but will stick to softmax in this post). The term “Fully Connected” implies that every neuron in the previous layer is connected to every neuron on the next layer. I recommend reading this post if you are unfamiliar with Multi Layer Perceptrons.
The output from the convolutional and pooling layers represent high-level features of the input image. The purpose of the Fully Connected layer is to use these features for classifying the input image into various classes based on the training dataset. For example, the image classification task we set out to perform has four possible outputs as shown in Figure 14 below (note that Figure 14 does not show connections between the nodes in the fully connected layer)
Figure 14: Fully Connected Layer -each node is connected to every other node in the adjacent layer
Apart from classification, adding a fully-connected layer is also a (usually) cheap way of learning non-linear combinations of these features. Most of the features from convolutional and pooling layers may be good for the classification task, but combinations of those features might be even better [11].
The sum of output probabilities from the Fully Connected Layer is 1. This is ensured by using the Softmax as the activation function in the output layer of the Fully Connected Layer. The Softmax function takes a vector of arbitrary real-valued scores and squashes it to a vector of values between zero and one that sum to one.
Putting it all together – Training using Backpropagation
As discussed above, the Convolution + Pooling layers act as Feature Extractors from the input image while Fully Connected layer acts as a classifier.
Note that in Figure 15 below, since the input image is a boat, the target probability is 1 for Boat class and 0 for other three classes, i.e.
Figure 15: Training the ConvNet
The overall training process of the Convolution Network may be summarized as below:
The above steps train the ConvNet – this essentially means that all the weights and parameters of the ConvNet have now been optimized to correctly classify images from the training set.
When a new (unseen) image is input into the ConvNet, the network would go through the forward propagation step and output a probability for each class (for a new image, the output probabilities are calculated using the weights which have been optimized to correctly classify all the previous training examples). If our training set is large enough, the network will (hopefully) generalize well to new images and classify them into correct categories.
Note 1: The steps above have been oversimplified and mathematical details have been avoided to provide intuition into the training process. See [4] and [12] for a mathematical formulation and thorough understanding.
Note 2: In the example above we used two sets of alternating Convolution and Pooling layers. Please note however, that these operations can be repeated any number of times in a single ConvNet. In fact, some of the best performing ConvNets today have tens of Convolution and Pooling layers! Also, it is not necessary to have a Pooling layer after every Convolutional Layer. As can be seen in the Figure 16 below, we can have multiple Convolution + ReLU operations in succession before having a Pooling operation. Also notice how each layer of the ConvNet is visualized in the Figure 16 below.
Figure 16: Source [4]
Visualizing Convolutional Neural Networks
In general, the more convolution steps we have, the more complicated features our network will be able to learn to recognize. For example, in Image Classification a ConvNet may learn to detect edges from raw pixels in the first layer, then use the edges to detect simple shapes in the second layer, and then use these shapes to deter higher-level features, such as facial shapes in higher layers [14]. This is demonstrated in Figure 17 below – these features were learnt using a Convolutional Deep Belief Network and the figure is included here just for demonstrating the idea (this is only an example: real life convolution filters may detect objects that have no meaning to humans).
Figure 17: Learned features from a Convolutional Deep Belief Network. Source [21]
Adam Harley created amazing visualizations of a Convolutional Neural Network trained on the MNIST Database of handwritten digits [13]. I highly recommend playing around with it to understand details of how a CNN works.
We will see below how the network works for an input ‘8’. Note that the visualization in Figure 18 does not show the ReLU operation separately.
Figure 18: Visualizing a ConvNet trained on handwritten digits. Source [13]
The input image contains 1024 pixels (32 x 32 image) and the first Convolution layer (Convolution Layer 1) is formed by convolution of six unique 5 × 5 (stride 1) filters with the input image. As seen, using six different filters produces a feature map of depth six.
Convolutional Layer 1 is followed by Pooling Layer 1 that does 2 × 2 max pooling (with stride 2) separately over the six feature maps in Convolution Layer 1. You can move your mouse pointer over any pixel in the Pooling Layer and observe the 2 x 2 grid it forms in the previous Convolution Layer (demonstrated in Figure 19). You’ll notice that the pixel having the maximum value (the brightest one) in the 2 x 2 grid makes it to the Pooling layer.
Figure 19: Visualizing the Pooling Operation. Source [13]
Pooling Layer 1 is followed by sixteen 5 × 5 (stride 1) convolutional filters that perform the convolution operation. This is followed by Pooling Layer 2 that does 2 × 2 max pooling (with stride 2). These two layers use the same concepts as described above.
We then have three fully-connected (FC) layers. There are:
Notice how in Figure 20, each of the 10 nodes in the output layer are connected to all 100 nodes in the 2nd Fully Connected layer (hence the name Fully Connected).
Also, note how the only bright node in the Output Layer corresponds to ‘8’ – this means that the network correctly classifies our handwritten digit (brighter node denotes that the output from it is higher, i.e. 8 has the highest probability among all other digits).
Figure 20: Visualizing the Filly Connected Layers. Source [13]
The 3d version of the same visualization is available here.
Other ConvNet Architectures
Convolutional Neural Networks have been around since early 1990s. We discussed the LeNet above which was one of the very first convolutional neural networks. Some other influential architectures are listed below [3] [4].
In this post, I have tried to explain the main concepts behind Convolutional Neural Networks in simple terms. There are several details I have oversimplified / skipped, but hopefully this post gave you some intuition around how they work.
This post was originally inspired from Understanding Convolutional Neural Networks for NLP by Denny Britz (which I would recommend reading) and a number of explanations here are based on that post. For a more thorough understanding of some of these concepts, I would encourage you to go through the notes from Stanford’s course on ConvNets as well as other excellent resources mentioned under References below. If you face any issues understanding any of the above concepts or have questions / suggestions, feel free to leave a comment below.
All images and animations used in this post belong to their respective authors as listed in References section below.