The ‘!’ notation is the factorial. As you might see, for non-negative integer x, it is calculated as the multiplication of all numbers up to x, for example:
2.2. The binomial density funtion (PMF)
Now, we are ready to define the binomial density function as a probability of obtaining m successes in N Bernoulli trails:
So, the binomial distribution is a discrete probability distribution of the number of successes (m) in a sequence of N independent repetitions of a given experiment, which asks yes-no (success-failure, 1–0) question, the probability of success is p, and the failure’s probability is q=1-p.
Let’s consider an example. You are practicing free throws during basketball training. From the season statistics, we know that the probability that you will score a point is 75%. Your coach told you that if you score 17 points out of 20 attempts, you will start for the next match. What is the probability that you score exactly 17 points?
We need to assume that the probability of a successful free throw shot is independent of the previous result (the mental strength does not play a role here). We also do not care about the order of scoring, such that it does not matter whether you fail first, third or last shot. Thus, this is a binomial distribution. We can use the binomial density function as given above and get:
We can repeat this excercise for other scores. As a result, we get the binomial distribution plot (PDF):

But you want to score at least 17 points, not exactly 17 points. So what is the probability that you will be in starting lineup for the next match?
2.3. The cumulative density funtion (CDF)
Here, a cumulative distribution function of a binomial distribution will help to answer this question. If you wonder why, please check this article first:
The cumulative distribution function (CDF) describes the probability (chance) that X will take a value equal to or less than k. The CDF function for the binomial distribution is as follows:
where [k] is the “floor” under k, i.e. the greatest integer equal to or less than k.
So, we need to sum the probabilities that you will score 17, 18, 19, or 20 free throw shots, as marked in red in the PMF plot:
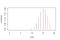
Since the probabilities sum to 1, we could also take the opposite approach – subtract cumulative probability of scoring maximum 16 points (all left from 17) from 1:
This is shown in the CDF plot:
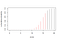
The result from both approaches matches. The task given by your coach is challenging but doable considering probability, so give it a try!
3. The behavior of binoimal distribution
How do the chances change if you get more attempts from your coach? You still have to achieve 85% of successful throws but you received 20, 50, or 100 trials. Let’s see the next plot.
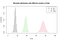
The higher the sample size, the wider the distribution. The probability od getting at least 85% of successfull free throws is as follows:
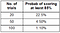
Considering the results in the table, you should not push your trainer to give you additional trials. The more attempts, the less likely is a better score than your long-term probability of success.
This content was originally published here.