Welcome to the August edition of V-hub, where we delve into the intricate world of technology. This month, we’ll be exploring the nested set model, a powerful data structure commonly used to represent hierarchical relationships.
From organizational charts to commenting systems, the nested set model offers a flexible and efficient way to store and manage hierarchical data. But, what does that mean?
Today, Vinova’s sharing our expert on nested set model, by Otis. Learn the A to Z of how to design the nested set model. Let’s dig in!
Table of Contents
1. Introduction
In modern data management systems, handling and managing hierarchical data is a common challenge.
Hierarchical data appears in various scenarios, such as:
- Directory Tree: File systems with nested directories and files.
- Product Catalog: Classification systems for products with categories and subcategories.
- Family Tree: Genealogy systems representing family relationships across generations.
- Organizational Chart: Describing the structure of personnel with departments and employees at different management levels.
Common issues when managing hierarchical data include:
- Query Efficiency: Retrieving all child elements of a parent node or all parent elements of a child node can require complex and time-consuming queries.
- Updating Tree Structure: Adding, modifying, or deleting a node in the tree can necessitate adjustments to multiple relationships, making maintenance complex.
- Performance with Large Data: When the number of nodes in the tree is large, operations on the data can become sluggish and difficult to optimize.
2. Common Methods for Implementing Tree Structures
2.1 The Adjacency List Model (Parent-Child Model)
With this model, we use the parent field to save the ID of the parent node.
Example:
| id | name | parent_id |
| 1 | Viet Nam | null |
| 2 | Ho Chi Minh City | 1 |
| 3 | Thu Duc City | 2 |
| 4 | Binh Thanh district | 2 |
| 5 | Go Vap district | 2 |
| 6 | Ha Noi Capital | 1 |
| 7 | Ba Dinh district | 6 |
| 8 | Cau Giay district | 6 |
| 9 | Da Nang City | 1 |
| 10 | Ward 17 | 5 |
Viet Nam node has parent_id is null, which means it does not have a parent node. Ho Chi Minh City, Da Nang City, and Ha Noi Capital have parent_id is 1, which is the id of the Viet Nam node.
Thus, Ho Chi Minh City, Da Nang City, and Ha Noi Capital node are the children of the Viet Nam node. Similarly, we can represent the table below as follows:
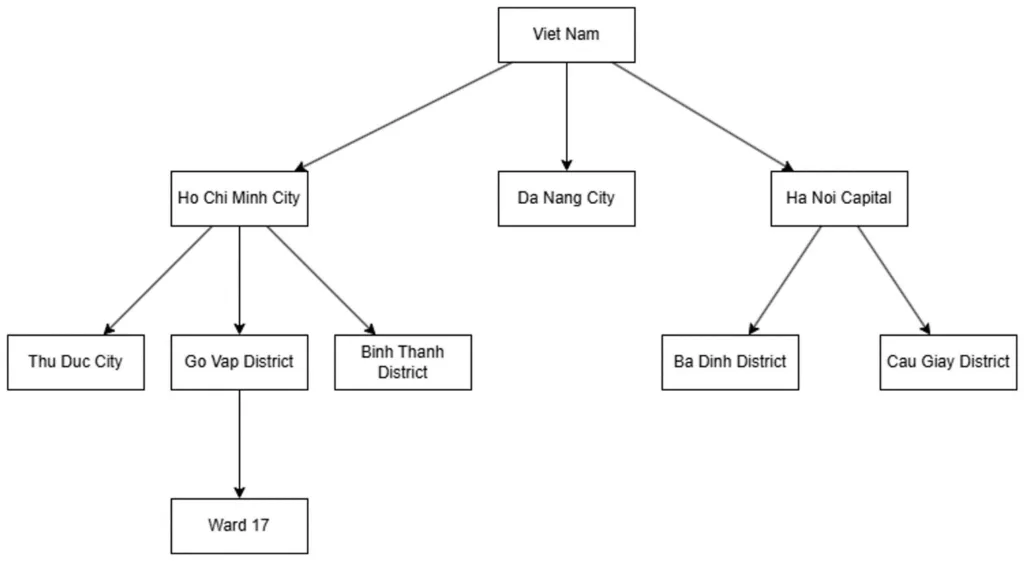
Advantages:
- Clear organization: Hierarchical structure makes it easy to manage and retrieve data.
- Inheritance: Allows reuse of properties and methods from the parent class.
- Easy to extend: Modify and extend child classes without affecting the parent.
- Access control: Easily define access rights for child classes.
- Simple structure: Helps users easily understand and interact with the system.
Disadvantages:
- Complex when changing: Changing the parent class can affect all child classes.
- Dependency: Child classes may become overly dependent on the parent class.
- Poor performance: Data retrieval in hierarchical structures can be slow.
- Difficulty managing loops: Dependency loops can be problematic.
- Challenging to fine-tune: Adjusting the properties of a child’s class without affecting the parent can be difficult.
2.2 Materialized Path
This model looks like The Adjacency List Model, but it uses the path field to save the path from the root node instead of the parent_id field.
Example:
| id | name | path |
| A | Viet Nam | A |
| B | Ho Chi Minh City | AB |
| C | Thu Duc City | ABC |
| D | Binh Thanh district | ABD |
| E | Go Vap district | ABE |
| F | Ha Noi Capital | AF |
| G | Ba Dinh district | AFG |
| H | Cau Giay district | AFH |
| K | Da Nang City | AK |
| L | Ward 17 | ABEL |
Therefore, the path of a node is the path of the parent node concatenated with the node’s ID.
We can represent the table below as follows:
Advantages:
- Simple Implementation: Easy to understand and implement.
- Efficient Reads: Fast retrieval of ancestors or descendants.
- No Recursive Queries: Simplifies hierarchy queries.
- Flexible: Adapts well to varying hierarchy depths.
- Compact Storage: Often requires less space than other models.
Disadvantages:
- Costly Updates: Updating nodes requires updating paths for all descendants.
- Path Length Limit: May struggle with very deep hierarchies.
- String Operations: Less efficient than numeric operations.
- Inconsistency Risk: Easy to introduce errors during updates.
- Complexity in Deep Hierarchies: Long paths can lead to management and performance issues.
2.3 Nested set model
In this post, I would like to introduce a different approach known as the Nested Set Model.
Instead of viewing our hierarchy as just nodes and lines, the Nested Set Model allows us to see it as a series of nested containers.
Imagine our data structured this way:
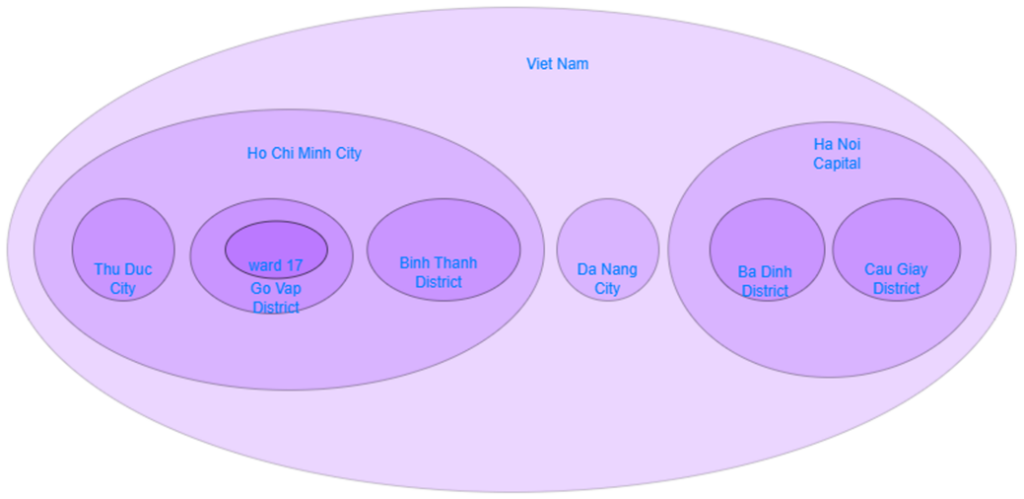
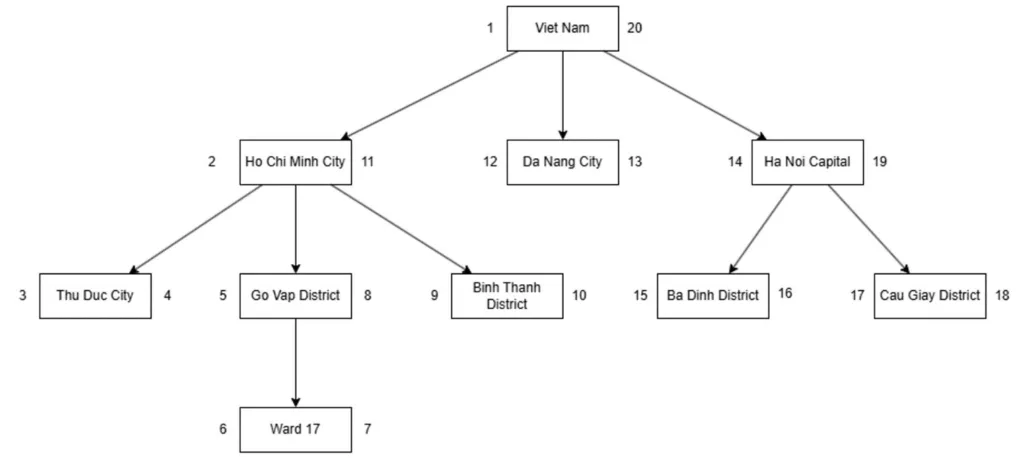
Notice how the hierarchy is still maintained, with parent node encompassing their children. This structure is visually represented in a table using left and right values to demonstrate the nested nodes.
Each node is traversed twice and is numbered according to the traversal order, from left to right, starting from the left side of the outer node, and continuing to the right.
The following is the numbering order after traversing all the nodes:
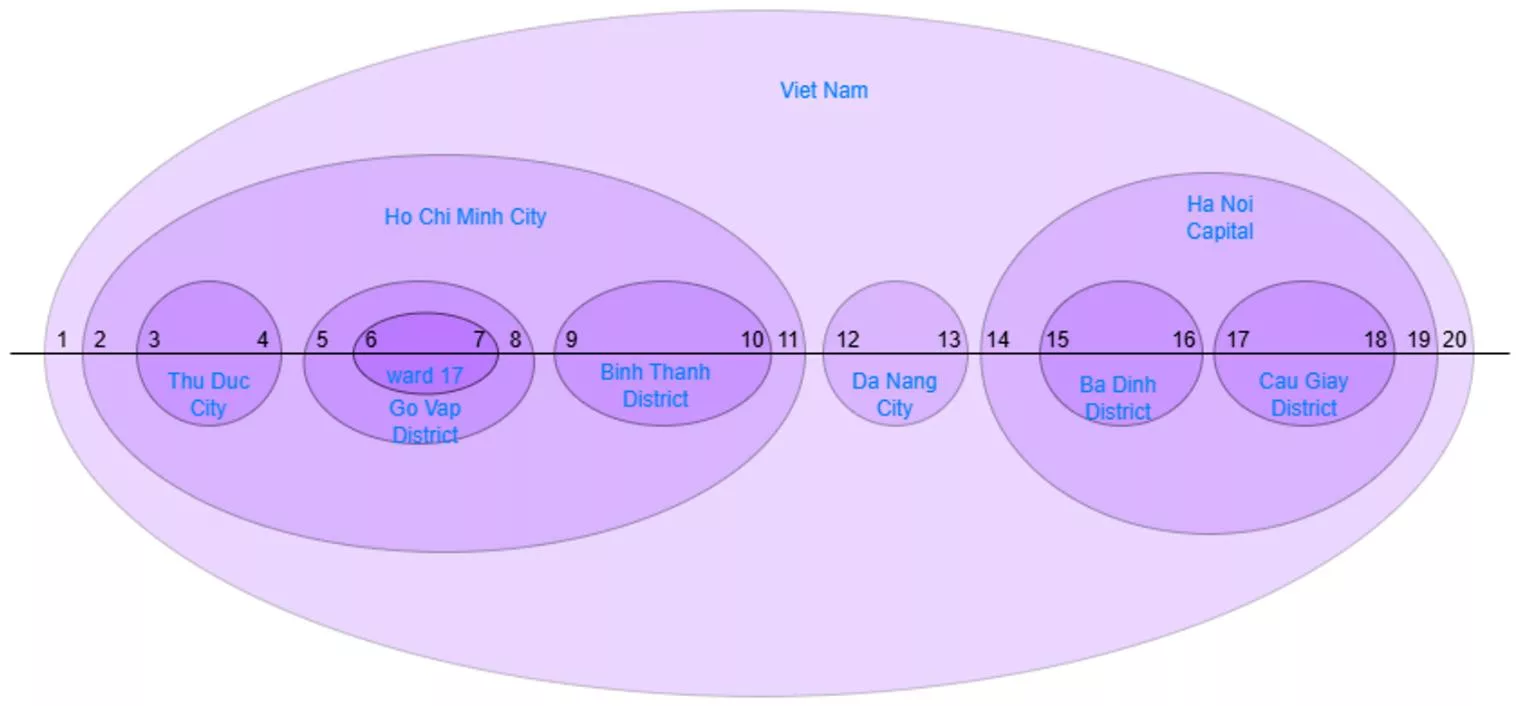
Based on that, we can easily query the position of the nodes.
From the above image, we will represent the data in a table to better visualize how this model works:
| id | name | left | right |
| 1 | Viet Nam | 1 | 20 |
| 2 | Ho Chi Minh City | 2 | 11 |
| 3 | Da Nang City | 12 | 13 |
| 4 | Ha Noi Capital | 14 | 19 |
| 5 | Thu Duc City | 3 | 4 |
| 6 | Go Vap District | 5 | 8 |
| 7 | Binh Thanh District | 9 | 10 |
| 8 | Ba Dinh District | 15 | 16 |
| 9 | Cau Giay District | 17 | 28 |
| 10 | Ward 17 | 6 | 7 |
This design can be applied to a typical tree as well:
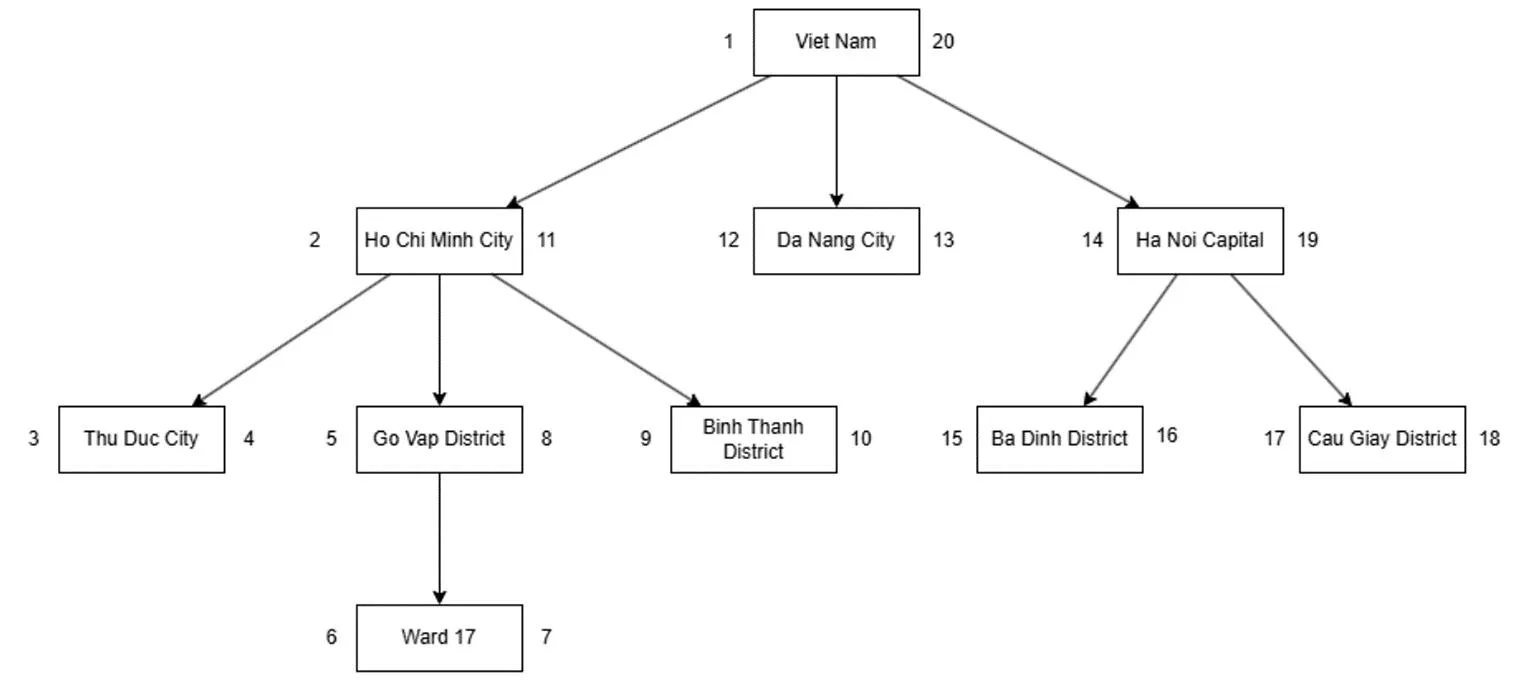
When working with a tree, we move from left to right, layer by layer, going down to each node’s children before assigning a right-hand number and then moving on. This method is known as the modified preorder tree traversal algorithm.
Advantages:
- Efficient Reads: Fast for querying entire subtrees or ancestors.
- No Recursive Joins: Simplifies hierarchical queries.
- Static Data: Works well with infrequently modified hierarchies.
- Easy to Query: Simple to retrieve hierarchical relationships.
- Fixed Storage Size: Predictable storage usage with left and right values.
Disadvantages:
- Expensive Updates: Costs increase with frequent insertions, deletions, or moves.
- Complex Management: Difficult to manage with frequent changes.
- Database Locking: This can lead to locking issues with frequent updates.
- Non-Intuitive: Left-right values can be hard to understand.
- Rebuild Costs: Significant changes require costly rebuilds of the hierarchy.
3. Here are some algorithms for implementing the Nested Set Model.
I will prepare a table structure and some sample data in PostgreSQL.
CREATE TABLE nested_data (
id SERIAL PRIMARY KEY,
name VARCHAR(20) NOT NULL,
lft INT NOT NULL,
rgt INT NOT NULL
);
INSERT INTO nested_data ( NAME, lft, rgt ) VALUES
( 'Viet Nam', 1, 20 ),
( 'Ho Chi Minh City', 2, 11 ),
( 'Da Nang City', 12, 13 ),
( 'Ha Noi Capital', 14, 19 ),
( 'Thu Duc City', 3, 4 ),
( 'Go Vap District', 5, 8 ),
( 'Binh Thanh District', 9, 10 ),
( 'Ba Dinh District', 15, 16 ),
( 'Cau Giay District', 17, 28 ),
( 'Ward 17', 6, 7 );3.1 Retrieving a Full Tree
We can get the entire tree using a self-join that connects parents with their nodes, since a node’s left value will always be between its parent’s left and right values.
-- Retrieving a Full Tree
SELECT
node.id,
node.name
FROM
nested_data AS node,
nested_data AS parent
WHERE
node.lft BETWEEN parent.lft AND parent.rgt
AND parent.name = 'Viet Nam'
ORDER BY node.lft;So, we have this result:

3.2 Adding New Nodes
Since each node stores its left and right values, adding a new node requires creating extra memory space for it, with a gap of 2 units.
Example: If we want to add a new node under the Da Nang City node, the new node would have left and right values of 13 and 14, with the left value of Da Nang City being incremented by 1 and the right value by 2.
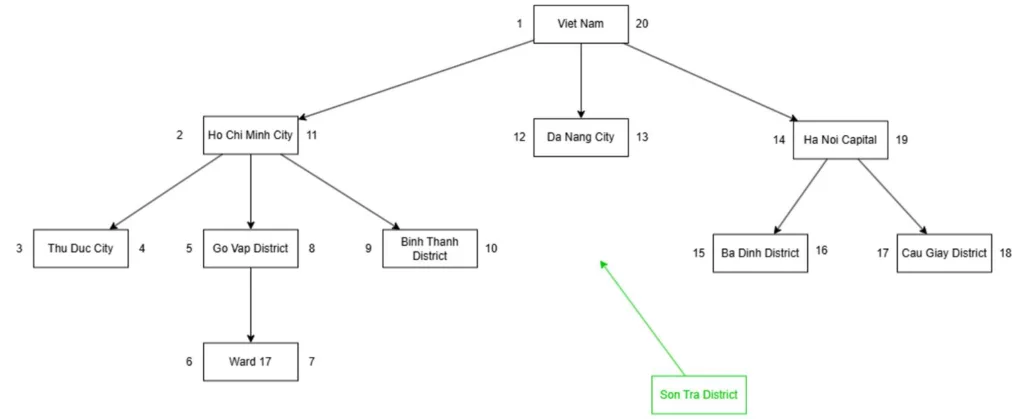
All nodes to their right would then have their left and right values increased by 2 including the right of that node. After that, we would insert the new node with the appropriate left and right values.
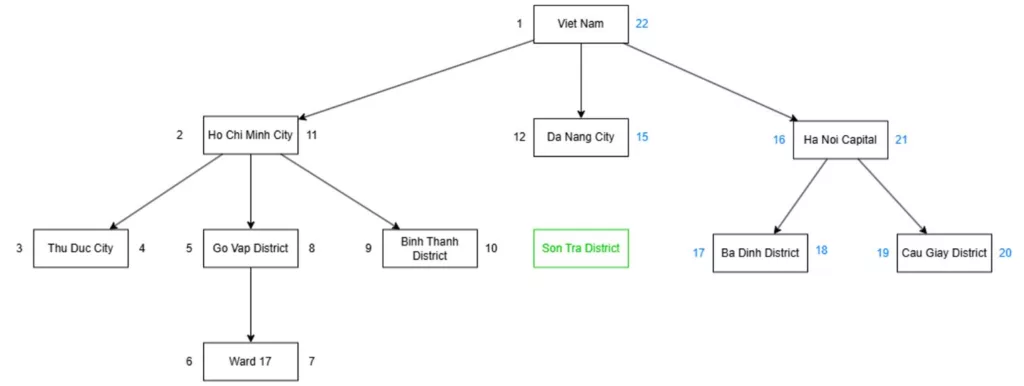
After inserting a new node.
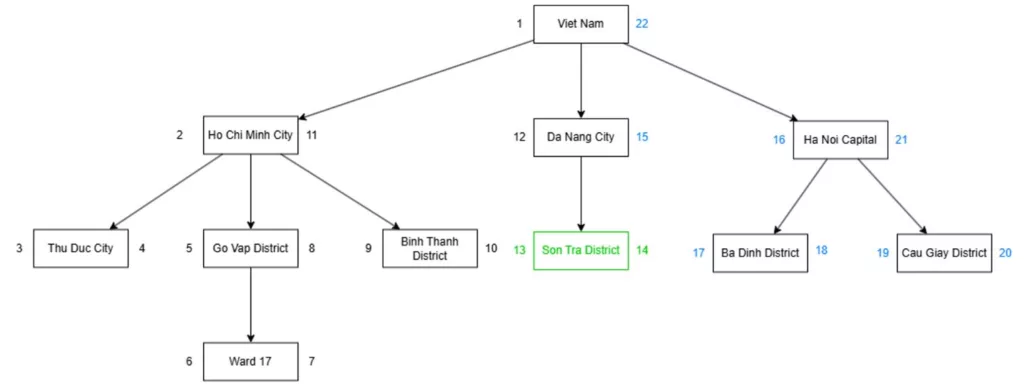
Implement with SQL:
DO $$
DECLARE
myRight INT;
BEGIN
-- Lock the rows for update
SELECT rgt INTO myRight
FROM nested_data
WHERE name = 'Da Nang City'
FOR UPDATE;
-- Update existing rows
UPDATE nested_data
SET rgt = rgt + 2
WHERE rgt >= myRight; -- use `>` if insert a new node between 2 other nodes
UPDATE nested_data
SET lft = lft + 2
WHERE lft > myRight;
-- Insert the new row
INSERT INTO nested_data(name, lft, rgt)
VALUES ( 'Son Tra District', myRight, myRight + 1 ); -- +1 if insert a new node between 2 other nodes
END $$;
Now you can use Retrieving a Full Tree to view the new data.
3.3 Deleting Nodes
If you want to delete a node, you need to update the left and right values for all nodes to the right of that node by a quantity of right – left + 1.
If the node being deleted is not a leaf node, then all its child nodes will be deleted as well.
Example: Remove the Da Nang City node that contains a child node.
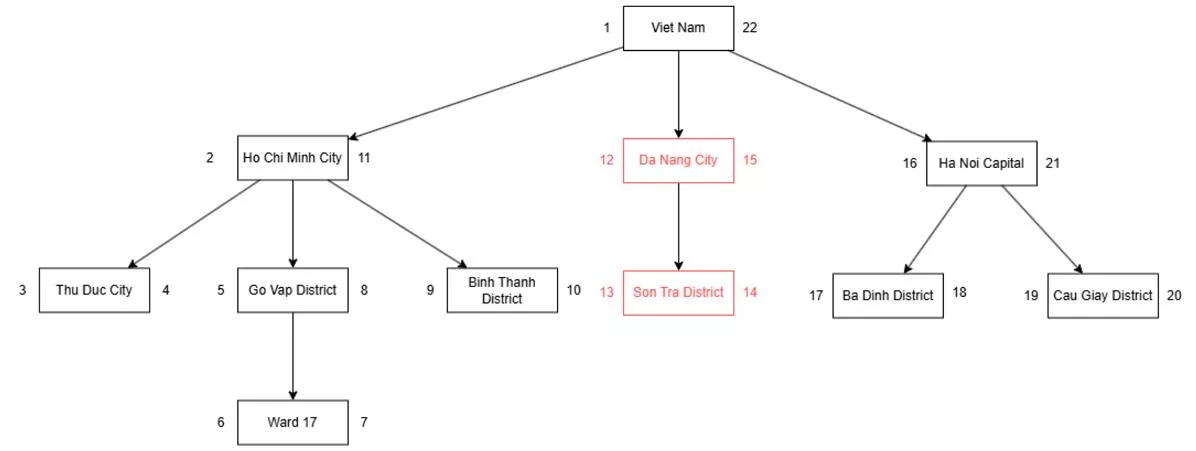
Step 1: Delete that node and its children.
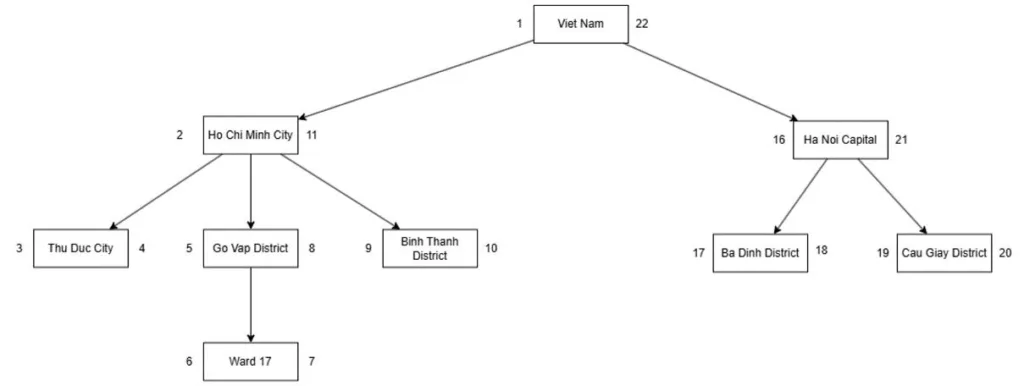
Step 2: Update the left and right values for all nodes to the right of that node.
Decrease (15 – 12 + 1) = 4 units.
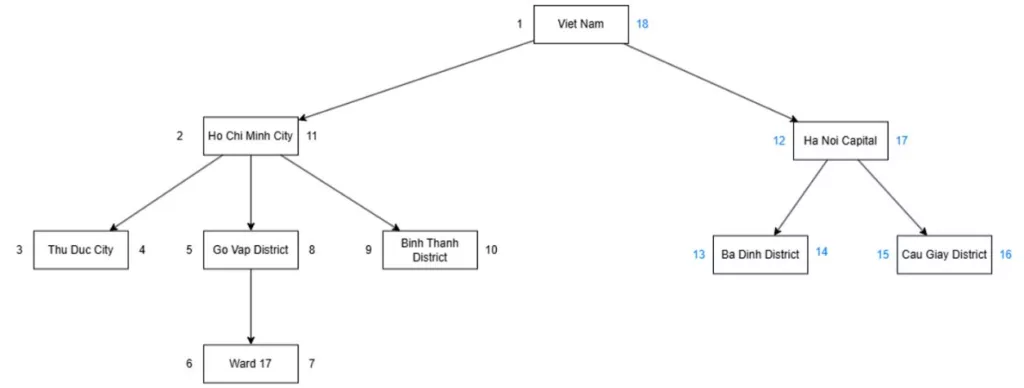
Implement with SQL:
-- Deleting Nodes
DO $$
DECLARE
myLeft INT;
myRight INT;
myWidth INT;
BEGIN
-- Lock the rows for update
SELECT lft, rgt, (rgt - lft + 1) INTO myLeft, myRight, myWidth
FROM nested_data
WHERE name = 'Da Nang City'
FOR UPDATE;
-- Delete the rows
DELETE FROM nested_data
WHERE lft BETWEEN myLeft AND myRight;
-- Update the remaining rows
UPDATE nested_data
SET rgt = rgt - myWidth
WHERE rgt > myRight;
UPDATE nested_data
SET lft = lft - myWidth
WHERE lft > myRight;
END $$;Now you can use Retrieving a Full Tree to view the new data.
4. Final Thoughts
- The Adjacency List Model (Parent-Child Model) structure is simple to implement, but it can cause query performance to slow down, especially with data that has more than two levels of depth. This slowdown happens because it is not possible to retrieve all the data with just one query. For instance, in a tree with five levels of depth, you would need to make four queries to get the information from the top node.
- Both the Materialized Path and Nested Set Model are more complex to implement. Insertions and updates are laborious and complex in these models, but they excel in data retrieval efficiency.
Despite its intricate logic, the Nested Set Model provides rapid data retrieval by utilizing the left and right values of nodes.
Consider choosing a model that suits your specific needs and the complexity of your dataset. The Adjacency List Model (Parent-Child Model) works well for simple data with few levels where quick retrieval is not a priority. On the other hand, for datasets with multiple levels requiring fast access, the Materialized Path and Nested Set Models would be more beneficial.
5. References / Resources
Managing Hierarchical Data in MySQL — Mike Hillyer’s Personal Webspace